DOI: https://doi.org/10.34069/AI/2025.86.02.12
Volume 14 - Issue 86: 147-163 / February-december, 2025
How to Cite:
Pineda León, E., Martinez Zayas, J.R., Flores Méndez, E., & Susarrey Huerta, O. (2025). Creep strain behaviour under seismic loads in reinforced concrete silos at high temperatures . Amazonia Investiga, 14(86), 147-163. https://doi.org/10.34069/AI/2025.86.02.12
Creep strain behaviour under seismic loads in reinforced concrete silos at high temperatures
Comportamiento de la deformación por fluencia plástica bajo cargas sísmicas en silos de concreto reforzado a altas temperaturas
Received: February 18, 2025 Accepted: May 10, 2025
Written by:
Ernesto Pineda León
https://orcid.org/0000-0002-2231-0080
PhD Instituto Politécnico Nacional, México. WoS Researcher ID: R-4753-2018 - Email: epinedal@ipn.mx
Jose Raul Martinez Zayas
https://orcid.org/0000-0002-7105-5434
MS Instituto Politécnico Nacional, México. WoS Researcher ID: GQB-2318-2022 - Email: jmartinezz1300@alumno.ipn.mx
Esteban Flores Méndez
https://orcid.org/0000-0003-0827-2820
PhD Instituto Politécnico Nacional, México. WoS Researcher ID: MCK-6564-2025 - Email: esfloresm@ipn.mx
Orlando Susarrey Huerta
https://orcid.org/0000-0003-3347-6438
PhD Instituto Politécnico Nacional, México. WoS Researcher ID: MFJ-9548-2025 - Email: osusarrey@ipn.mx
Abstract
This study investigates the creep behavior of a typical concentric conical hopper concrete silo used in Guerrero, Mexico, at high temperatures, comparing its response under static and seismic loading conditions. Primary creep deformation over 210 days was analyzed using the Time-Hardening Law, followed by a 20-year secondary creep analysis using Norton’s Power Law. Seismic loads were simulated through time-history analysis using a synthetic acceleration signal. The results, along with the comparison between seismic and non-seismic scenarios, highlight the significant influence of seismic events on long-term creep deformation and stress redistribution in concrete silos, with implications for the design and maintenance of these structures in seismically active regions.
Keywords: Concrete creep, dynamic response, finite elements, silos, time-dependent analysis.
Resumen
Este estudio analiza el comportamiento por fluencia de un silo de concreto con tolva cónica concéntrica, típico en Guerrero, México, sometido a altas temperaturas, comparando su respuesta ante condiciones de carga estática y sísmica. La deformación por fluencia primaria durante 210 días fue evaluada utilizando la Ley de Endurecimiento por Tiempo, seguida de un análisis de fluencia secundaria a 20 años mediante la Ley de Norton. Las cargas sísmicas se simularon mediante un análisis en el dominio del tiempo utilizando una señal de aceleración sintética. Los resultados, junto con la comparación entre los escenarios sísmico y no sísmico, destacan la influencia significativa de los eventos sísmicos en la deformación por fluencia a largo plazo y en la redistribución de esfuerzos en silos de concreto, con implicaciones para el diseño y mantenimiento de estas estructuras en regiones sísmicamente activas.
Palabras clave: Fluencia del concreto, respuesta dinámica, elementos finitos, silos, análisis dependiente del tiempo.
Introduction
Reinforced concrete silos are essential structures commonly used for storing bulk materials, particularly in the cement industry. Cement is typically stored at elevated temperatures, around 90 °C, after undergoing industrial processes such as crushing, homogenization, and kiln firing (Kok & Hui, 2011). Throughout their service life, these silos are subjected to both static and dynamic loading conditions, which can significantly affect their structural performance.
From a structural perspective, reinforced concrete silos are considered non-conventional systems due to their geometry and their tendency to exhibit nonlinear behavior under high stress concentrations (Nateghi & Yakhchalian, 2011). Structural failures in such systems are frequently attributed to the underestimation of seismic forces, wind-induced vortex effects, inadequate reinforcement detailing, insufficient stiffness, and the development of cracks, particularly in the upper third of the structure (Maraveas, 2020).
The elevated storage temperatures characteristic of cement silos significantly accelerates time-dependent phenomena such as creep, thereby compromising long-term structural integrity (Banerji & Kodur, 2022). Creep is defined as the progressive deformation of a material under sustained load and is closely associated with stress redistribution and the initiation and propagation of cracks (Su et al., 2017).
Creep is a nonlinear, time-dependent phenomenon typically categorized into three stages (Zhang et al., 2024): the primary stage, where the strain rate decreases over time; the secondary stage, characterized by a constant strain rate and the most substantial long-term deformations; and the tertiary stage, where the strain rate accelerates rapidly, potentially leading to structural failure (Bu et al., 2023). This study adopts the basic creep theory, which neglects moisture exchange between the concrete and its surrounding environment (Le Roy et al., 2017).
In many parts of the world, the design of silos remains largely empirical due to the absence of unified and comprehensive regulatory frameworks. While certain standards do exist, they often differ substantially in scope and commonly overlook critical aspects. Beyond these codes, numerous countries, particularly in Latin America, lack specific regulations for silos and instead rely on general provisions for reinforced concrete structures. This fragmented regulatory landscape leads to inconsistent design practices, which can compromise both the safety and durability of these structures.
Despite advances in structural modeling and materials science, the design of reinforced concrete silos in Mexico continues to follow quasi-empirical approaches and lacks the support of dedicated regulatory codes. This practice has led to recurring structural issues, increased maintenance demands, and growing safety concerns in numerous cement silo installations (Alcocer & Castaño, 2008).
In seismic regions, understanding the combined effects of long-term creep and earthquake-induced loads is of paramount importance. Seismic events typically occur after a silo has been in service for an extended period, during which creep deformations are already present and influence the dynamic response by altering the initial conditions of motion (Ma & Wang, 2015).
This interaction affects stress redistribution, displacement patterns, and strain development, potentially exceeding the limits anticipated in design provisions (Torres et al., 2021). Furthermore, the elastic modulus of concrete decreases over time, further modifying the structure’s dynamic properties (Ma et al., 2016). Additionally, various damage mechanisms may reduce the effective cross-sectional area of the silo walls, exacerbating their structural vulnerability (Xiong et al., 2022).
Amid these complexities, the present study aims to perform a comprehensive numerical analysis of the interaction between creep and seismic loading in large reinforced concrete silos operating at elevated temperatures. The objective is to enhance understanding of their long-term structural behavior and to provide insight that supports the development of safer and more resilient design strategies.
Theoretical Framework or Literature Review
Literature Review
Silos in Mexico
The design and construction of large-scale reinforced concrete silos has long been a necessity in Mexico due to their versatility in supporting complex industrial processes. However, their design was historically constrained by the absence of specific national guidelines. It was not until 1969 that the Comisión Federal de Electricidad introduced the first Manual de Diseño de Obras Civiles, which incorporated procedures for analyzing and designing non-conventional structures across different regions of the country (Hernández, 2021). Although this manual has undergone continuous revisions and modifications, the procedures it outlines remain limited to basic structural analyses, lacking the tools necessary to capture nonlinear behavior or time-dependent effects (Ordaz & Meli, 2004).
This limitation reflects a broader issue, the predominantly empirical nature of silo design in Mexico. While adequate for basic performance requirements, these methods may overlook critical behaviors such as creep interacting with dynamic loads, especially in high-temperature environments or seismic zones. The gap between design practice and advanced structural modeling highlights the need for updated methodologies that can more accurately assess the long-term performance of these structures.
Creep in reinforced concrete silos
One of the most critical effects of creep in silos is the progressive increase in deformations, which alters the original distribution of stresses within the structure (Kawecki et al., 2022). This redistribution can lead to stress concentrations in vulnerable areas, particularly in the silo walls, where the combined influence of mechanical and thermal loads promotes the development of cracking, (Breslavsky & Chuprynin, 2021). These cracks not only reduce the structural capacity of the material but also serve as initiation points for localized failures that can propagate rapidly and compromise the global integrity of the structure (Modi et al., 2024). When combined with dynamic loads, such as seismic events, the degradation process is accelerated, raising serious concerns regarding structural safety and service life.
Despite the recognized importance of creep, existing studies often treat it as a secondary effect or analyze it in isolation from dynamic actions. For example, while Liu, Zhou, Zhang and Jiang (2021) directly link creep-induced deterioration to several structural failures, their work does not account for interactions with other unfavourable factors. Similarly, although current codes provide basic creep considerations, they fail to address its interaction with cyclic loads or the role of environmental factors such as temperature variations and humidity (Yu et al., 2022).
The current state of literature reveals the lack of comprehensive models that accurately capture the long-term behavior of creep under complex loading scenarios and specific environmental conditions (Reddy et al., 2023). Addressing this shortcoming is essential to ensuring structural resilience. Therefore, this study aims to address this gap by examining the complex effects of creep in reinforced concrete silos, an area still underexplored, through advanced numerical models and robust analytical methodologies that enhance the durability and reliability of these nonconventional structures.
Relationship between creep and dynamic loads
Creep, traditionally understood as the slow, time-dependent deformation of materials under constant load, plays a more complex and critical role in dynamic systems, particularly under seismic loading. Hetland & Simons (2010) observed that post-seismic creep rates are influenced not only by time but also by the discrepancy between the total slip expected during a seismic cycle and the sum of coseismic slip and transient post-seismic creep. This finding suggests that conventional models may fail to fully capture the nuances of fault behavior under seismic stress. Moreover, while typical post-seismic creep exhibits an initial peak followed by decay, certain frictional faults present delayed post-seismic creep, where rates initially remain low, then increase, and eventually fall below the plate convergence rate, highlighting the need for more adaptable modeling approaches.
Ma et al. (2016) examined the effects of sustained versus instantaneous loads and demonstrated that creep alters the mechanical properties of concrete over time, thereby affecting both static and dynamic responses. Their numerical analysis of an arch bridge showed that natural frequencies increase progressively over time due to creep effects. However, although their study underscores the importance of considering creep in dynamic analyses, it is limited to bridge structures. Similarly, Ma & Wang (2015) emphasized that neglecting long-term effects in seismic design can lead to a significant underestimation of structural responses. Yet, their findings are primarily based on analyses of CFST bridges, raising questions about their generalizability to other structural systems.
Despite the growing interest in the dynamic implications of creep, a notable gap remains in the literature concerning reinforced concrete silos. These structures differ substantially from bridges in geometry, loading distribution, and functional demands, and their long-term behavior under the combined influence of creep and seismic loading has not been thoroughly investigated.
Methodology
The study case is a silo with a concentric conical hopper is presented since, in addition to being one of the most popular geometries in recent years, it has been identified as one of the most efficient for storing large quantities of granular materials due to its mass flow that eliminates obstructions possibilities minimizing the material segregation (Picone, 2024). For this case study, the primary creep behaviour is evaluated over a period of 210 days, according to the parameters identified by ASTM International (2018) for the type of concrete used in the silo. Subsequently, a seismic load representative of a high-intensity earthquake is applied, followed by a comparison of the secondary creep development over 20 years with a scenario where dynamic loads are absent. This approach estimates the durability of the structure in both cases, thereby allowing the identification of how dynamic loads influence the development of creep.

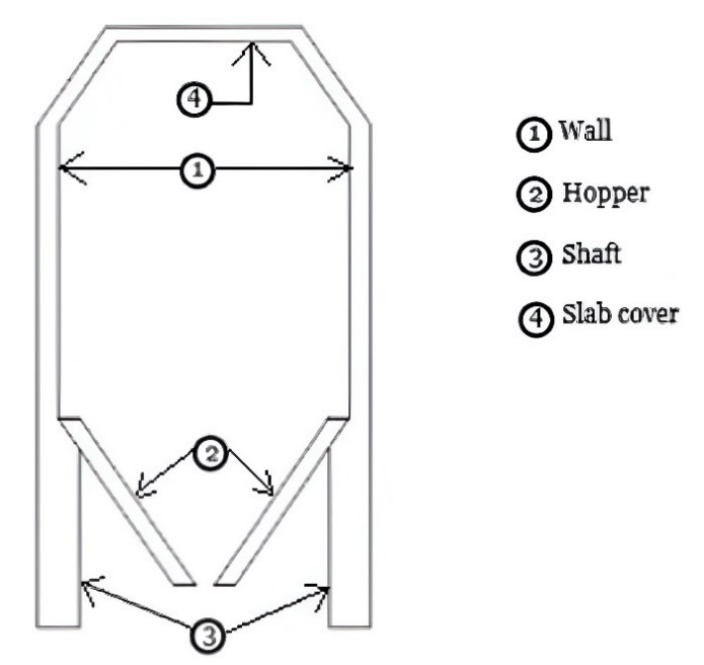
Figure 1. Silo longitudinal section.
Source: By the authors
Table 1.
Silo geometry.

This study case has 40 m height and 18 m diameter, presenting a height/diameter ratio of 2.22. The concentric conical hopper is 5 m height, presenting a discharge opening in its lower part with a 2.25 m diameter.
Table 2.
Reinforced steel arrangement in the wall.

Materials
Study cases proposed were carried out considering concrete at 28 days age with the mechanical properties shown in table 3.
Table 3.
Concrete mechanical properties.

Table 4.
Concrete mix used.

Grade 42 steel is used to reinforce the elements that make up the structural components of reinforced concrete silos. It meets the following parameters:
Table 5.
Reinforcing steel mechanical properties.
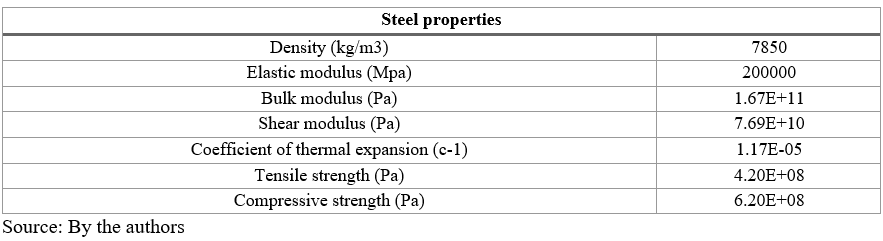
Creep behaviour laws
Numerical analysis of concrete creep is performed based on the two main implicit behaviour laws. The time hardening law has been shown to have great results in estimating primary creep at small periods of time. For the concrete used in these study models, it is known that primary creep phase ends after a period of 210 days (Bouziadi et al., 2020).
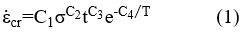
Where: C1, C2, C3, C4 – material constants, t – time, T – temperature, σ – stress
For a longer study time, Norton's law is capable to study the creep effects for long periods of time, evaluating the secondary phase.
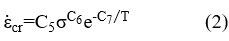
Where: C5, C6, C7 – material constants, T – temperature, σ – stress
Stored Material Properties
Stored material properties, such as the density, the angle of friction and the coefficient of friction, are considered according to the established parameters in the North American regulations, presenting the following magnitude (American Concrete Institute, 2016).
Table 6.
Stored materials properties.

Static loads
One of the most accurate and used ways to estimate static load conditions that the material will exert of the silo is through the Janssen method, which is based on the study of horizontal equilibrium layer of stored material this method is recommended by American Concrete Institute (2016). In this way the vertical loads at a depth Y are given by equation 3.
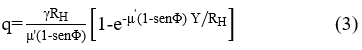
Where: Rh – hydraulic radius, Y – depth, γ – density, φ – angle of internal friction, μ´ – coefficient of friction against concrete.
The horizontal pressures known as ring stress for the case of silos of circular rein-forced concrete are calculated as:
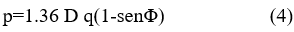
Where: D – silo diameter
Vertical friction per unit length is obtained from equation 5.

Based on the three mathematical expressions raised above, expressions are determined to obtain the existing loads in the silo hopper. Vertical pressure in this element is given by:

Where: q0 – silo diameter, hy – hopper depth
Normal pressure to the surface will be considered as the most unfavourable of equations 7 and 8.
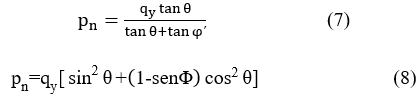
According to the expression used to calculate the normal pressure, it will be defined the calculation of the friction forces and will be chosen in a manner consistent with previous expressions.
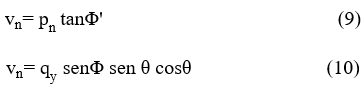
Dynamic loads
Every civil structure is subjected to various earthquake effects during its working life. Creep influence on dynamic behaviour due to seismic loadings is mainly originated by structural displacements, internal stresses and material properties which vary with time (Hetland & Simons, 2010). For this case, structural configuration silo presents an initial condition in which 210 days concrete primary creep is considered as initial condition for the successive time-history transient analysis. This numerical analysis is followed by a secondary creep study for 20 years and the results are compared between this case and the other one that no presents seismic loadings to verify how the earthquake presence affects the creep development. In this numerical model, cement mass vibrates convectively during seismic excitation and is connected to the impulsive mass to the silo wall, (Compagnoni et al., 2012). So, the general motion equation which solves the transient structural equilibrium is:
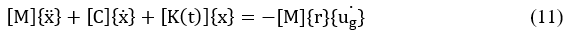
Where: [M] – mass matrix, [C] – damping matrix, {x} – displacement vector, {r}– unit influence vector, {üg}–ground acceleration, [K(t)]–stiffness matrix.
This silo case is placed in La Venta, in Mexico (16.4511 N, 98.7764 W), as is shown in figure 2. The soil is of granitic gneiss type, (Lázares, 2003). This corresponds to hard soil conditions Therefore, soil-structure interaction effects are neglected (Comisión Federal de Electricidad, 2015). An embedded support condition is assumed to represent the transfer of stresses to the foundation. The seismic design acceleration signal is obtained with the PRODISIS program, a program that was created and given by the Comisión Federal de Electricidad, 2015, in Mexico. The signal is obtained with a history time series in which the response spectrum matches the design spectrum. Figure 4 shows the synthetic used signal and is analysed in its frequency content through Short Fourier Transform (SFT).
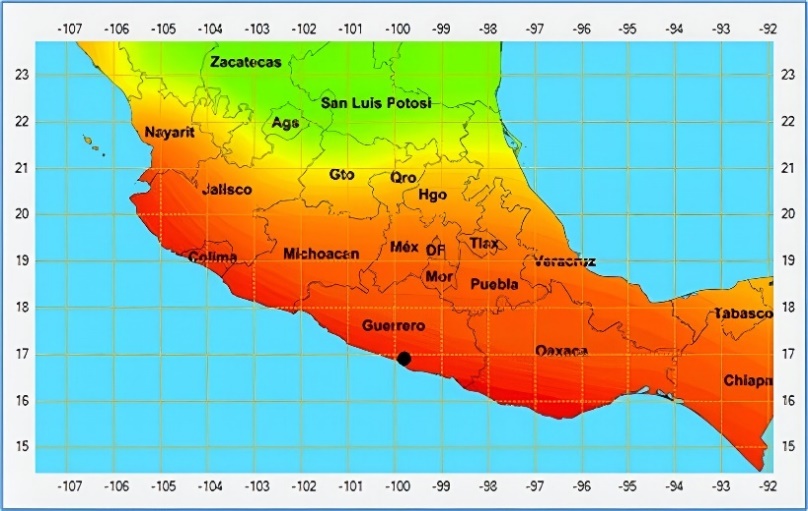
Figure 2. Seismic zone. La venta, Guerrero, México.
Source: Prodisis, Comisión Federal de Electricidad, 2015
The synthetic seismic signal generation process implemented in PRODISIS (Comisión Federal de Electricidad, 2015) employs stochastic signal techniques based on spectral and modal models (Clough & Penzien, 1993). The procedure begins with spectral modeling using a target design response spectrum obtained from the Federal Electricity Commission (CFE) seismic design guidelines. A signal is then constructed to match the specified frequency content of this target spectrum. Signal generation is performed through envelope modulation combined with random phase variables. The synthetic acceleration time history, a (t), is expressed as:
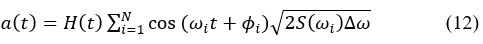
Where: H(t) is a trapezoidal-type function with exponential decay, simulating the energy buildup and decay of real earthquakes, is a random phase variable uniformly distributed, and is the target power spectral density (based on the desired response spectrum).
The generated signal is iteratively refined until its response spectrum closely matches the target design spectrum within a predefined tolerance.
The software internally, utilizes the following parameters: a seed signal recorded at the site, the target design spectrum corresponding to a specified return period, the total duration of the signal, the time step (Δt), frequency values and frequency range, both of which are defined based on the total duration and time step, and randomness in phase.
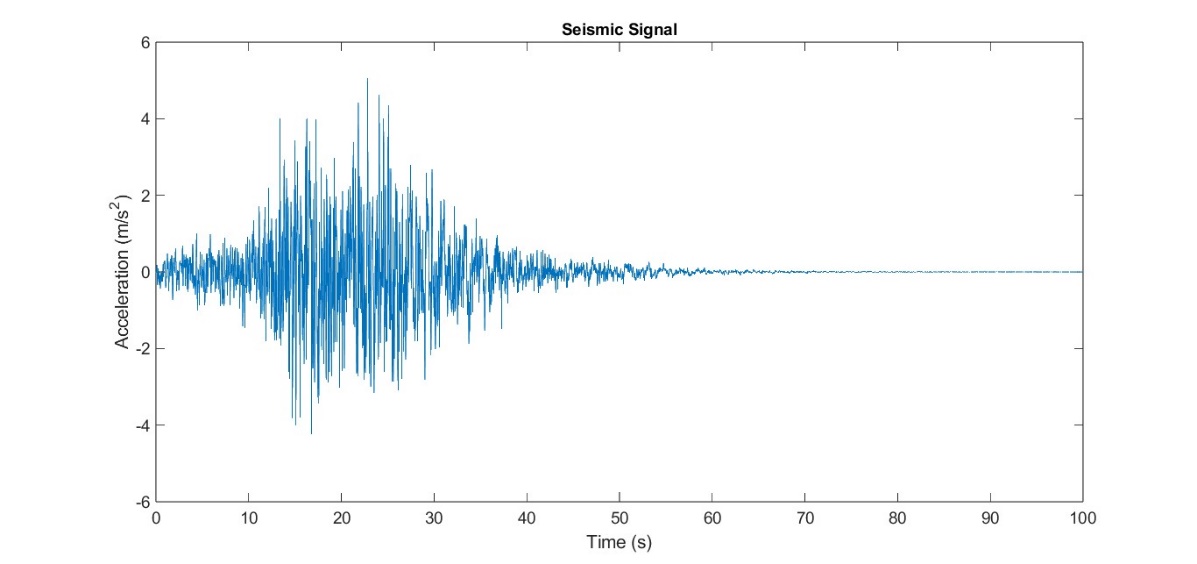
Figure 3. Applied synthetic signal.
Source: By the authors
The validation process consists of two stages. First, spectral match validation is performed by generating a family of synthetic earthquake records and comparing the average of their response spectra with that of the seed record. This comparison is typically required to achieve agreement within 10% (Comisión Federal de Electricidad, 2015; Vargas Colorado et al., 2022). Second, structural response validation is conducted by comparing the time-history responses of structural models subjected to both real and synthetic earthquakes. This step aims to verify statistical equivalence in key response parameters, such as peak displacement, peak acceleration, and energy demand (Guzmán Ventura et al., 2020; Vargas Colorado et al., 2022).
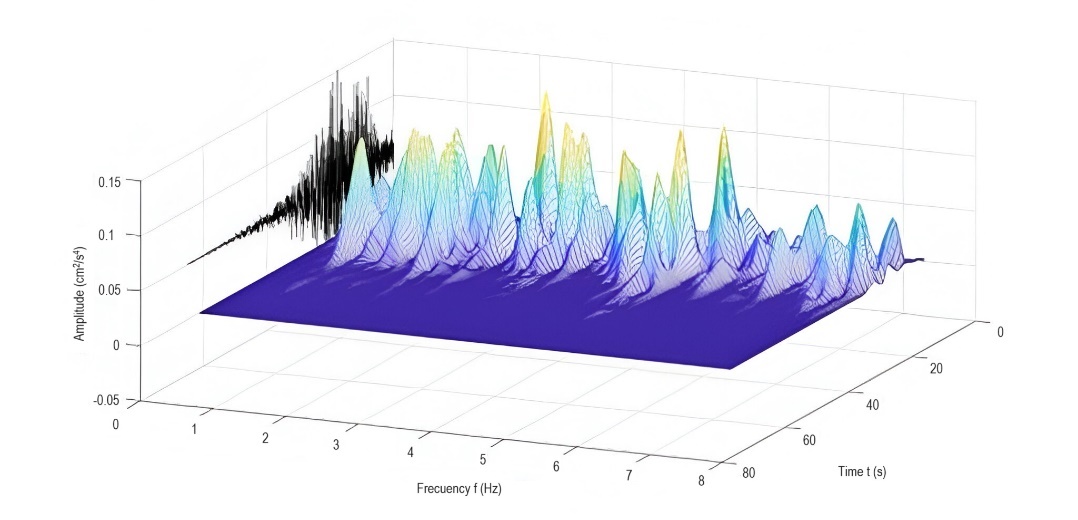
Figure 4. Short Fourier Transform of the seismic signal.
Source: By the authors
A Hamming window was used to obtain the SFT, the obtained surface was normalized to have the same energy that the signal has. When the silo is full, the fundamental period is T= 0.45 s, and its corresponding frequency is depicted with the frequency content of the signal given by its Fourier transform norm in figure 5. It is evident, that the seismic signal is going to demand the silo structure in an important matter.
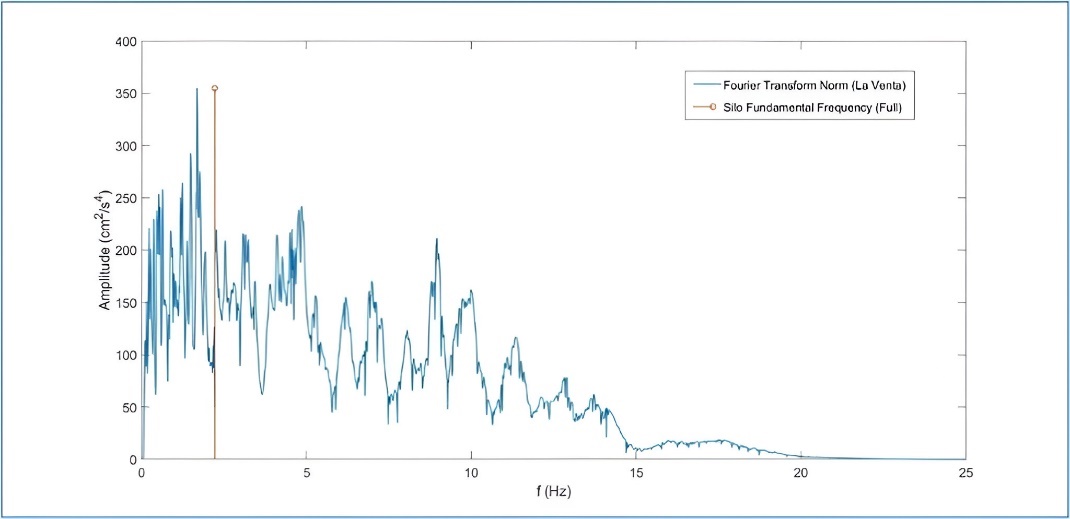
Figure 5. Silo frequency on the frequency content of the signal.
Source: By the authors
Results and Discussion
Numerical analysis is carried out with the finite element method, using Solid 186 element for concrete, a three-dimensional, higher-order solid element that excels at capturing complex stress and deformation patterns in continuum structures, supports geometric nonlinearity, and accommodates a wide range of advanced material models, including creep and temperature-dependent behaviors. Reinforcing steel is represented by Link 180 element types, a three-dimensional spar element transmits only axial forces between its nodes and supports geometric nonlinearity to accurately capture large strains. It also accommodates advanced material models, including creep and temperature-dependent behavior.
These materials interact in a contact surface between them, making the mesh nodes coincide. Mesh is crafted for an optimized element size resulting in 7614 nodes and 1033 elements. For the application of the existing loads on the structures, each one was discretized in sections of 1 m height, to apply the loads calculated according to the expressions presented in section 2. A perfect embedment in the lower face of the shaft is considered to simulate the behaviour that the superstructure would have when it is linked to its respective foundation. Likewise, the study period is defined considering that the primary creep stage will take place within the first 210 days of analysis and its behaviour will be studied with Time Hardening law. For numerical study purposes, the primary stage is subdivided into 211 parts where the first of them will have one second duration and the linear-elastic case will be presented. The remaining 210 steps are equidistantly distributed in the time analysis and with the obtained results of these steps, various curves are plotted to understand how the creep phenomenon has behaved in these cases. Secondary creep will appear after seismic excitation and its development continues for the next 20 years.
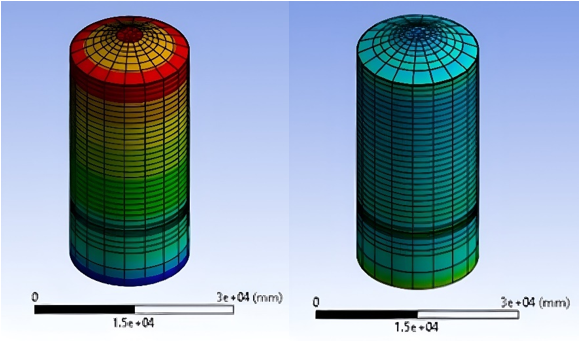
Figure 6. Total displacement at primary stage (left) and maximum principal strain at secondary stage (right).
Source: By the authors
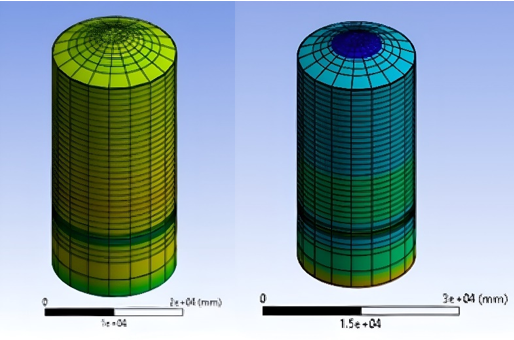
Figure 7. Middle principal strain and Equivalent creep strain at secondary stage.
Source: By the authors
Numerical analysis
Through the information treatment from the output files, it has been possible to identify the areas with the greatest unfavourable creep effects. These elements are located mainly in the wall, the hopper, and the shaft.
Table 7.
Most unfavourable elements ubication.
Primary Creep Results
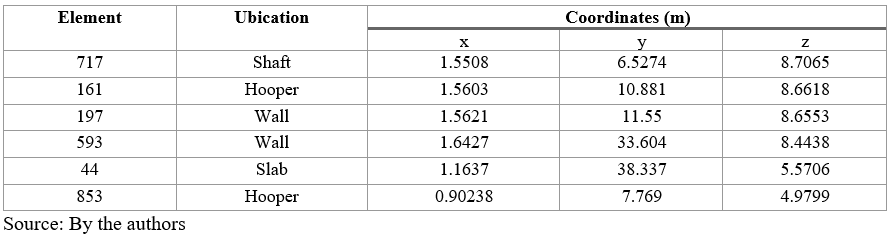
The best way to know the primary creep effects is studying the equivalent creep strain in the main elements of the silo. It is possible to identify how the elements present rapidly deformations that decreases with time. Primary creep strain results after 210 days are presented below.
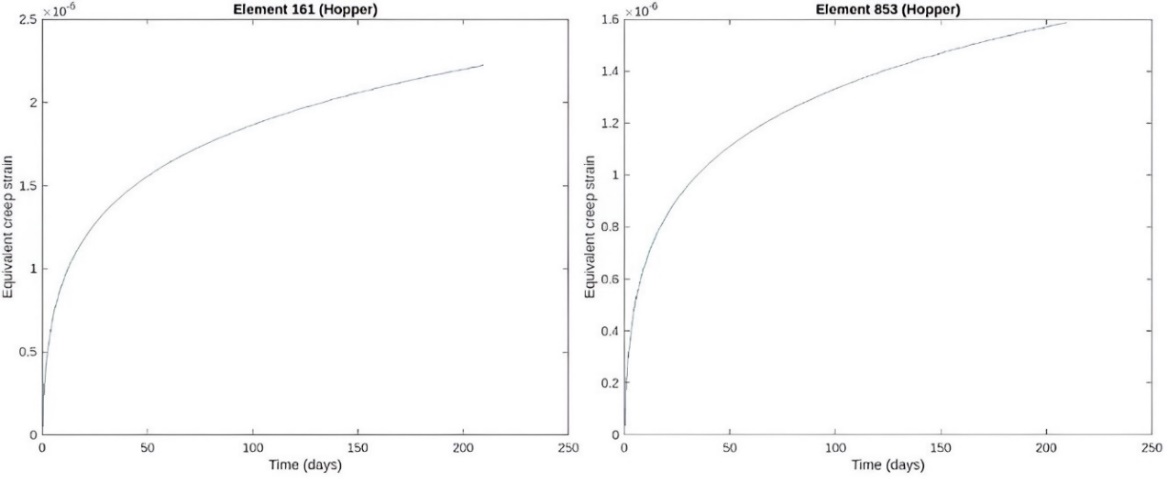
Figure 8. Equivalent primary creep strain in the hopper.
Source: By the authors
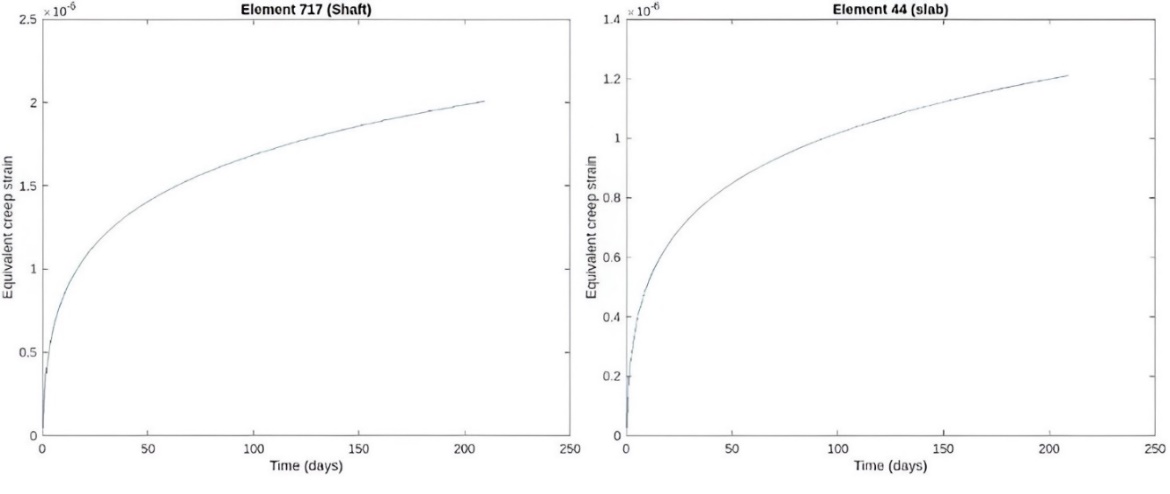
Figure 9. Equivalent primary creep strain in the shaft and the slab.
Source: By the authors
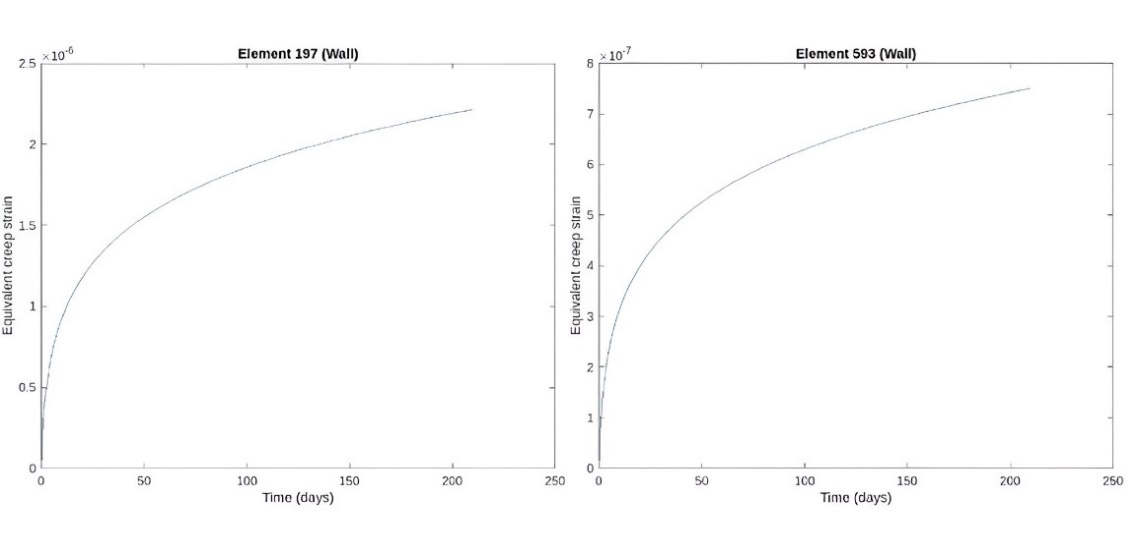
Figure 10. Equivalent primary creep strain in the wall.
Source: By the authors
Time-history analysis results
Seismic signal is applied in z direction after 210 days since the creep started. The numerical results show how the silo presents permanent deformation after the application of the accidental loads. The solution for the transient analysis is presented for the critical nodes.
Table 8.
Time-history analysis for critical nodes.


Figure 11. Permanent displacement after seismic load.
Source: By the authors
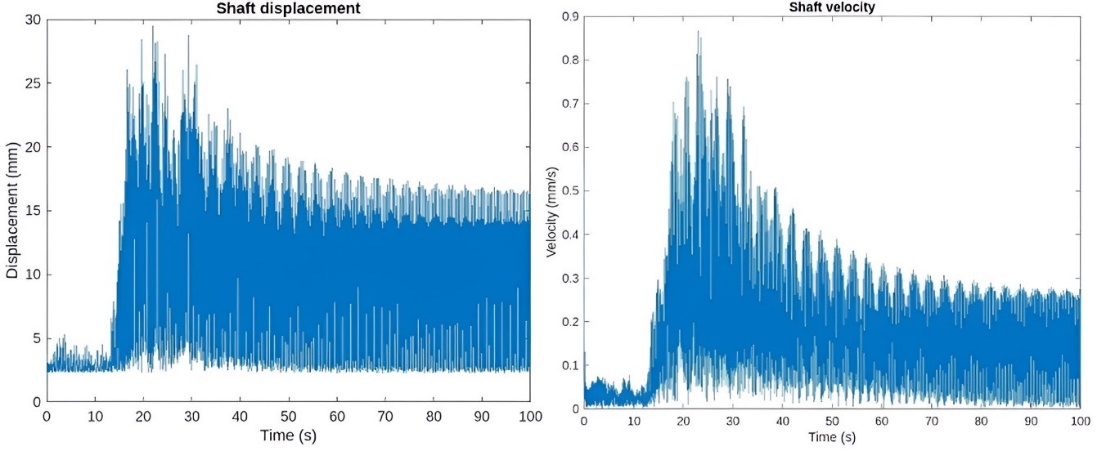
Figure 12. Dynamic response in the shaft.
Source: By the authors
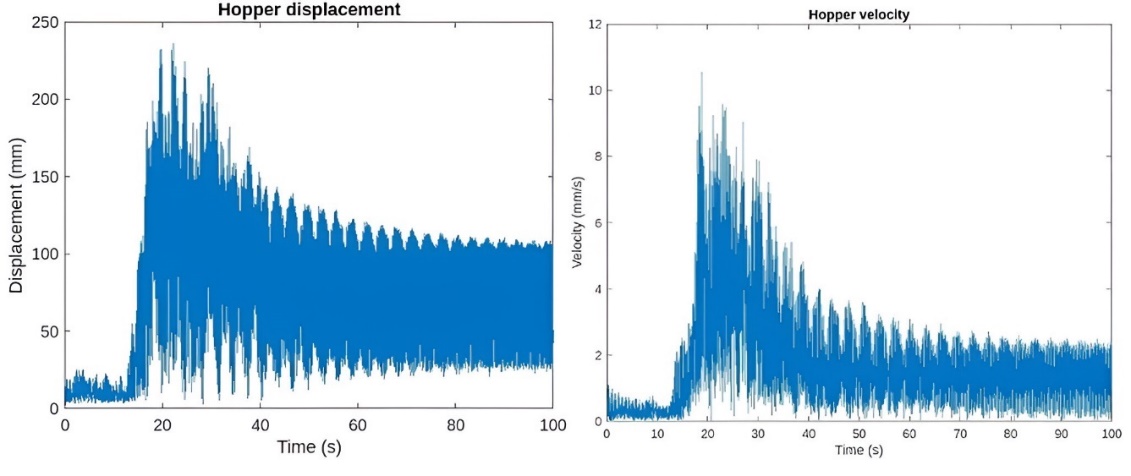
Figure 13. Dynamic response in the hopper.
Source: By the authors
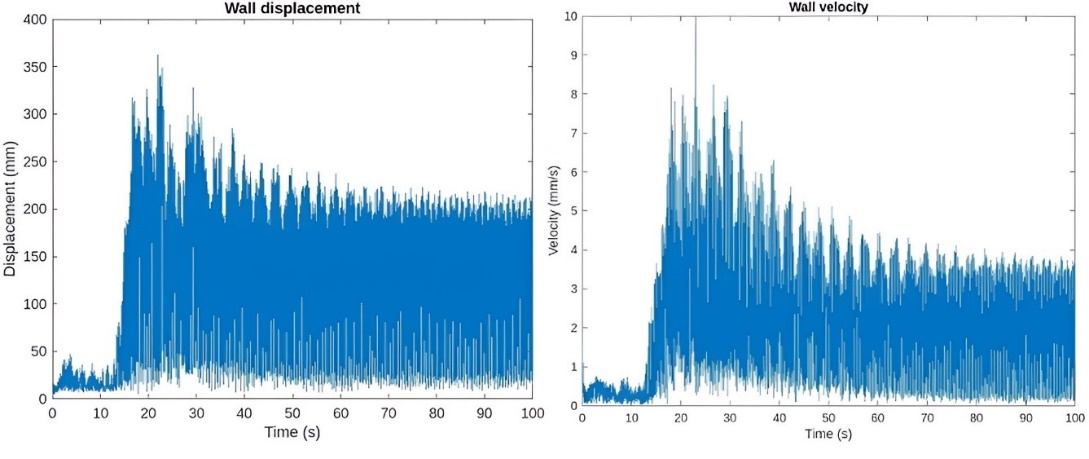
Figure 14. Dynamic response in the wall.
Source: By the authors
Secondary Creep results and comparison
For this stage analysis a comparison is presented where the first case is secondary creep after the seismic excitation, the second one is a stationary stage after primary creep, no seismic load is considered in this case. For both sceneries the analysis is done for 20 years, and the most relevant differences are presented below.
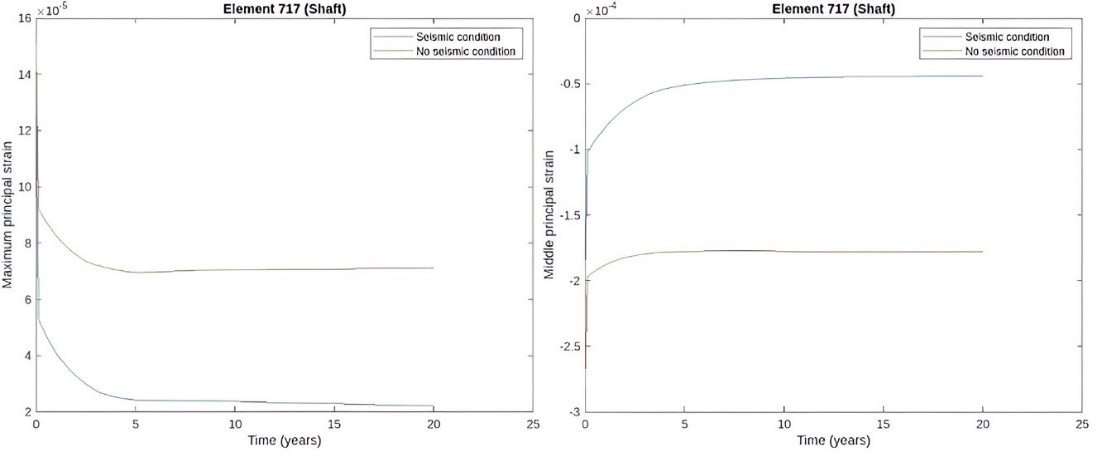
Figure 15. Secondary stage comparison in the shaft.
Source: By the authors
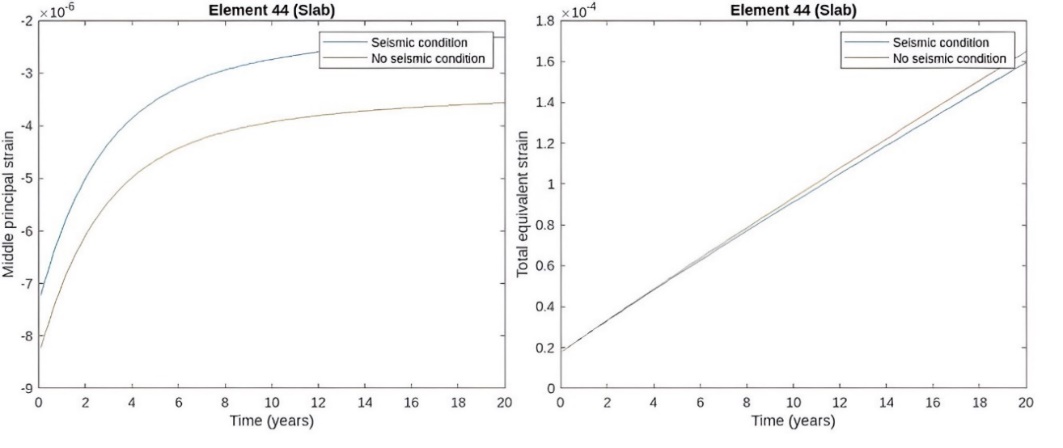
Figure 16. Secondary stage comparison in the slab.
Source: By the authors
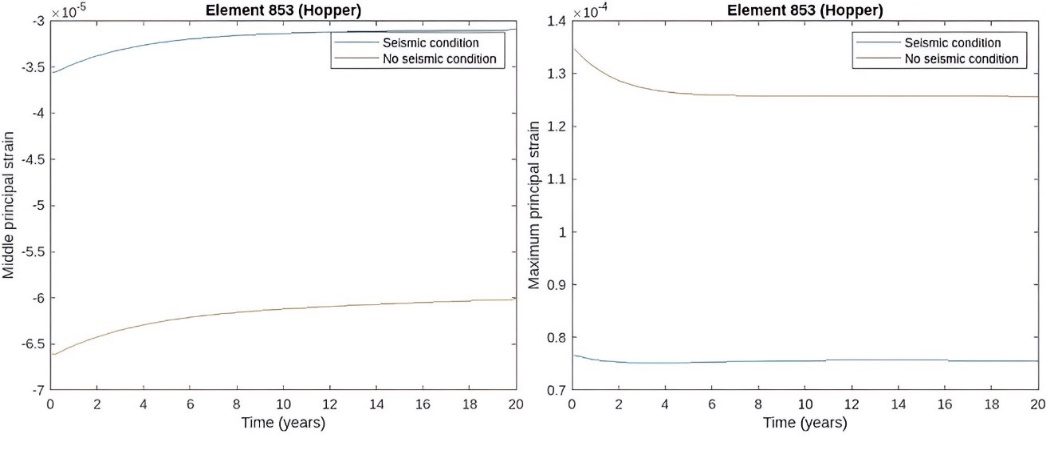
Figure 17. Secondary stage comparison in the hopper.
Source: By the authors
Influence of creep on natural frequencies
The calculation of the natural frequencies in the case study is carried out by considering the degradation of the modulus of elasticity over time, as well as the structural configuration for each of the proposed scenarios. It is demonstrated that the frequencies of the vibration modes increase, with a greater difference observed in the higher modes. It has been established that reinforced concrete silos exhibit vibration modes within a narrow frequency range; therefore, the error induced by disregarding the effects of creep could exceed the difference between two closely spaced frequencies.
Table 9.
Natural Frequencies for presented creep scenarios.
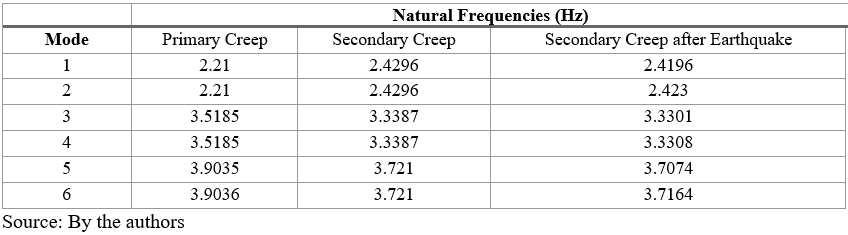
After 20 years of creep the frequencies rise 9.94%, 5.11%, 4.68% at modes 1,3 and 5 respectively. Secondary creep and secondary creep after earthquake rise 0.41% and 0.12%.
Conclusions
This study demonstrates that creep deformations significantly alter the stress distribution in reinforced concrete silos, with pronounced effects in the hopper, shaft, and wall. During the primary creep stage, numerical results show a slight increase in principal strains, accompanied by a degradation of the elastic modulus, which modifies the initial conditions for subsequent analyses. Although the level of deformation at this stage may appear similar to that predicted by linear-elastic analysis, its long-term implications become increasingly relevant, highlighting the importance of incorporating time-dependent material behavior in the design of durable structures.
The time-history analysis reveals that seismic loading induces permanent deformations and changes the state of stress from compression to tension in critical regions near the top of the shaft, increasing the likelihood of cracking, particularly in the shaft and hopper. Significant damage is expected in primary structural members, with possible failures in secondary elements. The wall undergoes the largest displacements in its lower third, while stress redistributions are concentrated in the hopper and shaft. These results reflect a critical scenario, as conventional seismic design manuals typically do not account for nonlinear behavior of large silos at this stage of service life.
Secondary creep further amplifies deformations, especially in the upper shaft and hopper, where displacements in the -y direction become significant. The progressive increase in ring stresses and mid-height principal strains evidences the continued deterioration of structural integrity. Compared to the non-seismic case, seismic excitation results in significantly greater long-term deformations due to the contribution of instantaneous loading. These findings suggest that seismic actions accelerate the progression of creep, potentially leading to earlier onset of critical damage and stability issues.
The combined effects of creep and seismic loading contribute to a progressive loss of stiffness, altering the dynamic response of the structure. Natural frequency analysis confirms that permanent seismic deformations disrupt the silo's axisymmetry, resulting in irregular vibration modes. This change in dynamic behavior may also imply the emergence of soil-structure interaction effects that are not captured by traditional linear-elastic analyses. Secondary creep is expected to continue altering the natural frequencies, exacerbating these issues over time.
Overall, this study underscores the necessity of explicitly considering both creep and seismic effects in the analysis and design of reinforced concrete silos. Neglecting these phenomena may lead to underestimated demands, reduced structural reliability, and increased risk of failure. Given the geometric and mechanical complexity of large silos in seismic zones and the current lack of design standards that adequately address these challenges there is a clear need for further research into the interaction between time-dependent concrete behavior and dynamic loads. Additionally, future work should include probabilistic reliability analyses to support the development of optimal design strategies for these critical structures.
Bibliographic references
Alcocer, S. M., & Castaño, V. M. (2008). Evolution of codes for structural design in Mexico. Structural Survey, 26(1), 17-28.
American Concrete Institute. (2016). ACI CODE-313-16: Design specification for concrete silos and stacking tubes for storing granular materials and commentary. https://acortar.link/EmTwkK
ASTM International. (2018). ASTM E139-11(2018) standard test methods for conducting creep, creep-rupture, and stress-rupture tests of metallic materials. https://www.astm.org/e0139-11r18.html
Banerji, S., & Kodur, V. (2022). Effect of temperature on mechanical properties of ultra‐high performance concrete. Fire and Materials, 46(1), 287-301.
Bouziadi, F., Boulekbache, B., Haddi, A., Hamrat, M., & Djelal, C. (2020). Finite element modeling of creep behavior of FRP-externally strengthened reinforced concrete beams. Engineering Structures, 204, 109908.
Breslavsky, D., & Chuprynin, A. (2021). Analysis of creep, shrinkage, and damage in armored concrete dome at static and seismic loading. Nonlinear Mechanics of Complex Structures: From Theory to Engineering Applications, 265-277.
Bu, P., Li, Y., Li, Y., Wen, L., Wang, J., & Zhang, X. (2023). Creep damage coupling model of concrete based on the statistical damage theory. Journal of Building Engineering, 63, 105437.
Clough, R. W., & Penzien, J. (1993). Dynamics of Structures. 2nd Edition. McGraw-Hill
Comisión Federal de Electricidad. (2015). Manual de obras civiles: Diseño de estructuras de concreto (Tomo 4). Comisión Federal de Electricidad.
Compagnoni, M. E., Curadelli, O., & Martínez, C. A. (2012). Análisis del comportamiento dinámico de tanques cilíndricos bajo excitación sísmica. Mecánica Computacional, 31(13), 2219-2230.
Guzmán Ventura, J. A., Williams Linera, F., Riquer Trujillo, G., Vargas Colorado, A., & Leyva Soberanis, R. (2020). Fallas de licuación de suelos inducidas por el sismo de Tehuantepec del 7 de septiembre de 2017 (Mw 8.2) en la Ciudad de Coatzacoalcos, Veracruz, México. Ingeniería sísmica, (102), 82-106.
Hernández, J. A. S. (2021). COMPARATIVO DE LOS MODELOS PARAMÉTRICOS DE ESPECTROS DE DISEÑO SÍSMICO CFE 2015 Y NTC 2020: COMPARISON OF THE PARAMETRIC MODELS OF SEISMIC DESIGN SPECTRA 2015 AND NTC 2020. Revista Pakbal, 1(01), 15-21.
Hetland, E. A., & Simons, M. (2010). Post-seismic and interseismic fault creep II: Transient creep and interseismic stress shadows on megathrusts. Geophysical Journal International, 181(1), 99-112.
Kawecki, B., Halicka, A., & Podgórski, J. (2022). Buckling of cylindrical concrete tanks and silos due to prestressing—nonlinear approach. Thin-Walled Structures, 176, 109339.
Kok, L. B., & Hui, Y. M. (2011). Protection of aged cement clinker silo against high impact and high temperature discharge. In Advances in FRP Composites in Civil Engineering: Proceedings of the 5th International Conference on FRP Composites in Civil Engineering (CICE 2010), Sep 27–29, 2010, Beijing, China (pp. 415-418). Berlin, Heidelberg: Springer Berlin Heidelberg.
Lázares, L. (2003). Respuesta sísmica y posible comportamiento no lineal del suelo en la Ciudad de México (Tesis de maestría). Universidad Nacional Autónoma de México, UNAM.
Le Roy, R., Le Maou, F., & Torrenti, J. M. (2017). Long term basic creep behavior of high performance concrete: data and modelling. Materials and structures, 50(1), 85.
Liu, W., Zhou, H., Zhang, S., & Jiang, S. (2021). Constitutive model of concrete creep damage considering the deterioration of creep parameters. Construction and Building Materials, 308, 125047.
Ma, Y. S., & Wang, Y. F. (2015). Creep influence on structural dynamic reliability. Engineering Structures, 99, 1-8.
Ma, Y. S., Wang, Y. F., Su, L., & Mei, S. Q. (2016). Influence of creep on dynamic behavior of concrete filled steel tube arch bridges. Steel & Composite Structures, 21(1), 109-122.
Maraveas, C. (2020). Concrete silos: Failures, design issues and repair/strengthening methods. Applied Sciences, 10(11), 3938.
Modi, M. A., Patel, K. A., & Chaudhary, S. (2024). Assessment of cracking, creep and shrinkage effects in indeterminate steel-concrete composite flexural members at service load. In Structures (Vol. 70, p. 107663). Elsevier.
Nateghi, F., & Yakhchalian, M. (2011). Seismic behavior of reinforced concrete silos considering granular material-structure interaction. Procedia Engineering, 14, 3050-3058.
Ordaz, M., & Meli, R. (2004). Seismic design and codes in Mexico. In Proceedings of the Thirteenth World Conference on Earthquake Engineering (CD-ROM). Canadian Association for Earthquake Engineering, Vancouver, BC, Canada (No. 4000).
Picone, T. (2024). Effectively Discharging Solid Materials from Storage Bins and Silos. Chemical Engineering, 131(4).
Reddy, V. M., Kumar, D. U., Aggarwal, S., & Prasad, G. V. S. (2023). Analysis and design of silos by the post-tensioned method. In E3S Web of Conferences (Vol. 430, p. 01018). EDP Sciences.
Su, L., Wang, Y. F., Mei, S. Q., & Li, P. F. (2017). Experimental investigation on the fundamental behavior of concrete creep. Construction and Building Materials, 152, 250-258.
Torres, P. P., Ghorbel, E., & Wardeh, G. (2021). Towards a new analytical creep model for cement-based concrete using design standards approach. Buildings, 11(4), 155.
Vargas Colorado, A., Barradas Hernández, J. E., Williams Linera, F., Leyva Soberanis, R., Rivera Baizabal, R., & Riquer Trujillo, G. (2022). Construcción de espectros de sitio y regionales para estructuras convencionales en la conurbación Veracruz-Boca del Río, empleando una adaptación del procedimiento recomendado en el CDS-MDOC-2015 para construir espectros de sitio. Ingeniería sísmica, (SPE108), 53-78.
Xiong, Z., Zhang, R., Ma, L., Hao, Z., Lv, W., & Li, W. (2022). Creep Prediction Model of Concrete-Filled Steel Tube under Different Core Concrete Conditions. In Journal of Physics: Conference Series (Vol. 2168, No. 1, p. 012006). IOP Publishing.
Yu, P., Li, R. Q., Bie, D. P., Yao, X. M., Liu, X. C., & Duan, Y. H. (2022). A coupled creep and damage model of concrete considering rate effect. Journal of Building Engineering, 45, 103621.
Zhang, D., Zhang, L., Lan, T., Wen, J., & Gao, L. (2024). A memory-dependent three-dimensional creep model for concrete. Case Studies in Construction Materials, 20, e03289.

https://amazoniainvestiga.info/ ISSN 2322- 6307
This article presents no conflicts of interest. This article is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). Reproduction, distribution, and public communication of the work, as well as the creation of derivative works, are permitted provided that the original source is cited.